論理回路
#20200527b
順序機械の話
- 「機械」と呼ばれる数学的な理論
- 有向グラフによって動作を記述
自販機の状態遷移
自販機の動作
簡単な自販機の動作を考える:
- 硬貨なしにボタンを押しても何もしない
- 100円硬貨を1枚だけ受け付ける
- それ以上入れた場合には硬貨を返却
自販機の状態変化
入力(ボタンor硬貨) →出力(点灯or商品) →状態の変化
| 入力 | 出力 | 状態 |
|---|---|---|
| 硬貨 | 商品選択ボタン点灯 | 商品選択ボタン待機 |
| 商品選択ボタン | 商品を出力 | 硬貨待機 |
ドリップコーヒー自販機の動作
$B_1$: コーヒー選択ボタン,$B_2$: 砂糖の量ボタン,$B_3$: 抽出ボタン
| 入力 | 出力 | 状態 |
|---|---|---|
| 硬貨 | $B_1$点灯 | $B_1$待機 |
| $B_1$ | $B_2$点灯 | $B_2$待機 |
| $B_2$ | $B_3$点灯 | $B_3$待機 |
| $B_3$ | 抽出 & 扉を開口 | 取り出し待機 |
| 取り出し | 扉を閉口 | 硬貨待機 |
カウンタの動作
5進カウンタの動作を考える:
- 0,1,2,3,4を順に出力
- 4のあとは0を出力
- 入力はクロックパルス(CP)
カウンタの状態変化
入力(クロックパルス) →出力($0$~$4$) →状態の変化
| 入力 | 出力 | 状態 |
|---|---|---|
| CP | 0 | 1の出力を待機 |
| CP | 1 | 2の出力を待機 |
| CP | 2 | 3の出力を待機 |
| CP | 3 | 4の出力を待機 |
| CP | 4 | 0の出力待機 |
状態遷移図
状態遷移図とは
- 状態の変化を有向グラフで表したもの
- 各ノード$q_i$は状態を表す
- 各エッジは入出力に応じた状態の遷移を表す
- 入力 $i$と出力 $o$ に対応する遷移は $i/o$ というラベルがつく
簡単な自販機の場合
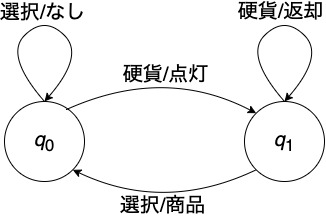
- $q_0$: 硬貨が入っていない状態
- $q_1$: 硬貨が入っている状態
ミーリーマシンとも呼ばれる
カウンタをミーリーマシンで表す
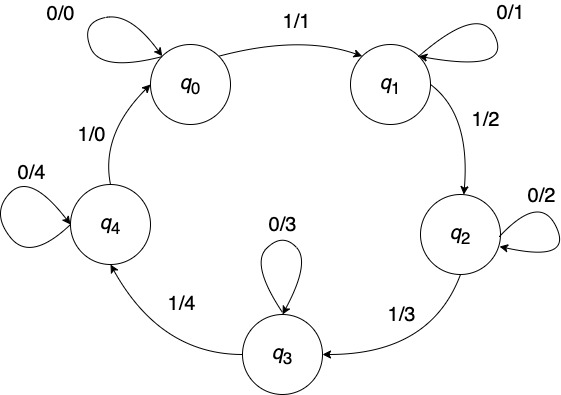
- $q_i$: $i$を出力し続ける状態($0\leq i\leq 4$)
カウンタをミーリーマシンで表す
- カウンタの出力は入力と無関係
- カウンタの出力を状態と同一視
各状態を出力と見做す:
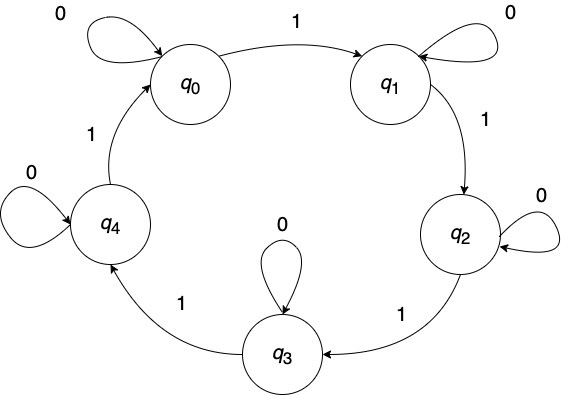
こちらはムーアマシンと呼ばれる
{ミーリー/ムーア}マシン
どちらも同じオートマトンです.
- 状態遷移図で表される
- 各ノードは状態を表す
- 各エッジは状態の遷移を表す
オートマトン
- 定義1(オートマトン)
- $\Sigma$ を記号の集合, $Q$を状態の集合, $\delta: Q\times \Sigma\to Q$を状態遷移関数, $F\subseteq Q$ を受理状態の集合とする. この時$(\Sigma, Q, \delta, q_00,F)$ を$\Sigma$上のオートマトンと呼ぶ. ただし$q_0\in Q$は開始状態を表す.
次回
- ミーリーマシンによる簡単化について
- 最終
テスト課題について