論理回路

#20200527a

復習

  • ブール代数と論理素子
  • FF回路

ブール代数

(2元)ブール代数とは

  • 0と1からなる演算
  • 掛け算と足し算が定義
  • 0の補元は1($\overline{0}=1$)
  • 1の補元は0($\overline{1}=0$)

(論理)積

  • $A$と$B$の掛け算: $A\cdot B$
  • $A\cdot B=\min (A,B)$
$_B\backslash ^A$ $0$ $1$
$0$ $0$ $0$
$1$ $0$ $1$
積の演算表

(論理)和

  • $A$と$B$の足し算: $A+ B$
  • $A+B=\max (A,B)$
$_B\backslash ^A$ $0$ $1$
$0$ $0$ $1$
$1$ $1$ $1$
和の演算表

補元

  • $A$の補元: $\overline{A}$
  • $\overline{A} = 1 - A$
$A$ $\overline{A}$
$0$ $1$
$1$ $0$
演算表

論理関数

  • ブール代数の式のこと
    • $F = A+B\cdot C$ などと表記
    • $A\cdot B$は$AB$と書いても良い
      • 積の優先順位は和よりも高いため

順序回路

  • 出力が入力や出力の時間順序に依存する回路を 順序回路 と呼ぶ

    • ある時点の状態と入力で次の出力が決定
    • 入力と直前の内部状態の関数で出力を表現
    • フリップフロップ(FF)回路とも

RS-FF

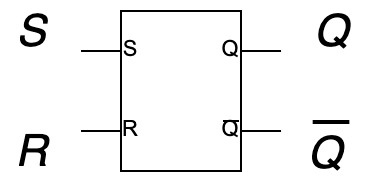
  • $S$と$R$は入力, $Q$と$\overline{Q}$は出力
  • 直前が$S=1$なら$Q=1$
  • 直前が$R=1$なら$Q=0$
  • $S=R=0$のとき, $Q$は直前の状態を記憶
    • $S=R=1$は禁止状態

RS-FFの動作を確認

https://yutomi7a.github.io/simcirjs/rsff.html

※上のRS-FFは負論理で実装されているため, NOTゲートを挟んで入力を反転させます.

RST-FF

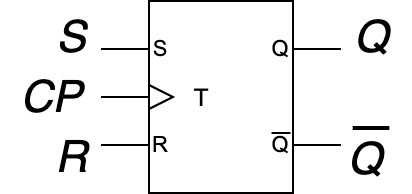
  • クロックパルス($CP$)の入力Tが追加
  • $CP＝1$の時のみSまたはRの入力が有効化
    • $CP=0$ならSとRは無視される

RST-FFの構造

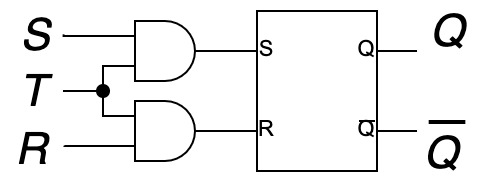
  • RS-FFの各入力に注目
    • $T\land S$ → S
    • $T\land R$ → R

JK-FF

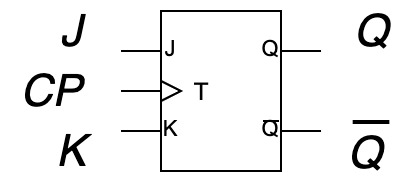
  • RST-FFを改良したもの
  • 直前が$J=1$なら$Q=1$
  • 直前が$K=1$なら$Q=0$
  • $J=K=0$のとき, $Q$は直前の状態を記憶
  • $J=K=1$のとき, $Q$は直前の状態を反転

JK-FFの動作を確認

https://yutomi7a.github.io/simcirjs/jkff.html

D-FF

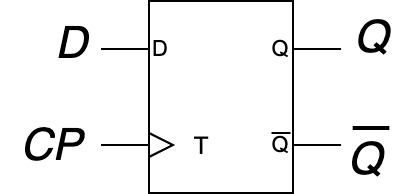
  • Dへの入力をずらして出力する回路
  • Tへの入力(CP)に合わせて出力
    • ポジティブエッジトリガーの場合には, Tが上がるタイミングで出力
    • ネガティブエッジトリガーの場合には, Tが下がるタイミングで出力

D-FFの動作を確認

https://yutomi7a.github.io/simcirjs/dff.html

上はネガティブエッジトリガーです.

カウンタ

カウンタの種類

  • 入力されるCPの数を一定まで数える順序回路

    • アップカウンタ: 1ずつ増加
    • ダウンカウンタ: 1ずつ減少

  • 典型的なのは $n$ビット$2$進カウンタ

    • アップカウンタなら, $2^n-1$まで数えたら$0$を出力
    • ダウンカウンタなら, $2^n-1$から数えて$0$まで出力

カウンタの設計

一般的なカウンタの(JK-FFを用いた)設計

  1. FFの各状態遷移に対する入力条件表を用意
  2. 拡大された状態遷移表(拡大入力要求表)を作成
  3. FFの入力の条件式を求める
  • カルノー図を使うことも多い

例題: $2$ビット$2$進アップカウンタ

  • $0\to 1\to 2\to 3\to 0\to\ldots$と推移
  • 二つのJK-FFを使用

JK-FFの状態遷移表

$J$ $K$ $T$ $Q^{t+1}$
0 0 $\rceil\hspace{-.39in}\downarrow\hspace{-.39in}\lfloor$ $Q^t$
0 1 $\rceil\hspace{-.39in}\downarrow\hspace{-.39in}\lfloor$ 0
1 0 $\rceil\hspace{-.39in}\downarrow\hspace{-.39in}\lfloor$ 1
1 1 $\rceil\hspace{-.39in}\downarrow\hspace{-.39in}\lfloor$ $\overline{Q^{t}}$
JK-FFの状態遷移表

状態遷移に対する入力条件表

$Q^t\to Q^{t+1}$ $J$の条件 $K$の条件 状態動作
$0\to 0$ $0$ - 保持/リセット
$0\to 1$ $1$ - 反転/セット
$1\to 0$ - $1$ 反転/リセット
$1\to 1$ - $0$ 保持/セット
状態遷移に対するJK-FFの条件

JK-FFの拡大状態遷移表

$Q_1^{t}$ $Q_{0}^{t}$ $Q_1^{t+1}$ $Q_{0}^{t+1}$ $J_1$ $K_1$ $J_0$ $K_0$
0 0 0 1 0 - 1 -
0 1 1 0 1 - - 1
1 0 1 1 - 0 1 -
1 1 0 0 - 1 - 1
JK-FFの拡大状態遷移表

ここから各JK-FFの$J$, $K$それぞれの条件式を求める

入力$J_1$の条件式を求める

ドントケア(-)は含めても含めなくとも良い
$_{Q^{t}_1}\backslash ^{Q^{t}_0}$ 0 1
0 0 1
1 - -
$J_1$の条件式

$J_1 = Q^{t}_0$

入力$J_0$の条件式を求める

なるべく大きなグループで囲む
$_{Q^{t}_1}\backslash ^{Q^{t}_0}$ 0 1
0 1 -
1 1 -
$J_0$の条件式

$J_0 = 1$

入力$K_1$の条件式を求める

ドントケア(-)は含めても含めなくとも良い
$_{Q^{t}_1}\backslash ^{Q^{t}_0}$ 0 1
0 - -
1 0 1
$K_1$の条件式

$K_1 = Q^{t}_0$

入力$K_0$の条件式を求める

なるべく大きなグループで囲む
$_{Q^{t}_1}\backslash ^{Q^{t}_0}$ 0 1
0 1 -
1 1 -
$J_0$の条件式

$K_0 = 1$

条件式から順序回路を構成

$J=K=1$とし, $Q_0$の出力を次の$J$と$K$に入力

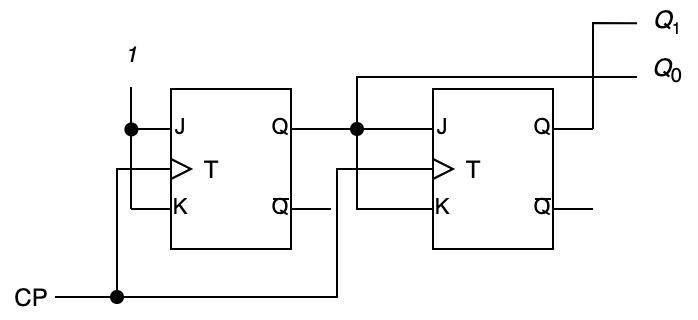
  • $N$進カウンタも設計可能
    • アップカウンタなら, $N-1$まで数えたら$0$を出力
    • ダウンカウンタなら, $0$の次に$N-1$を出力
    • 本日の課題として出題